Im Unterschied zu quasihomogenen und isotropen Wandbaustoffen wie Beton verhält sich Mauerwerk in alle Richtungen anders und trägt dabei auch unterschiedlich.
Die heute vermauerten Ziegel alleine sind schon anisotrop, wegen der Anforderungen an den Wärmeschutz ist nicht einmal das Lochbild in Wandlängsrichtung und quer dazu gleichmäßig. Das Vermauern mit einem sich gänzlich anders verhaltenden Baustoff, dem Mörtel, der zumeist nicht einmal die entstehenden vertikalen Stoßfugen füllt, verkompliziert die Situation noch weiter. Zu beachten ist, dass Mauerwerk wegen des schwachen Haftverbundes zwischen Stein und Mörtel nur eine geringe Biegezug- und fast keine Zugfestigkeit aufweist. Dabei ist die unterschiedliche Qualität der Vermauerung auf der Baustelle ein wesentlicher Einflussfaktor.
Parameter wie die Ziegelzugfestigkeit quer und längs sind in der Regel ebenfalls stark streuend oder werden oft gar nicht erhoben. Das Verformungsverhalten der beiden Wandbestandteile z.B. unter Druck unterscheidet sich ebenso wie das Verformungsverhalten von ganzen Wänden in den beiden Hauptrichtungen „Quer zur Fuge“ und „in Fugenlängsrichtung“.
Mauerwerk ist demnach ein komplexer Verbundwerkstoff, der aber große Vorteile durch seine Anpassbarkeit an örtliche Gegebenheiten, durch die einfache, kleinvolumige Herstellung und seinen stark handwerklichen Charakter aufweist. Wichtig ist jedoch eine sorgfältige Ausführung und hohe Herstellungsqualität, welche aber bei sorgsamer Überwachung und kompetenten Baufirmen problemlos erreicht werden kann.
Der Zusammenhalt von Mörtel und Ziegel beruht auf Bindungskräften zwischen den beiden Materialien bzw. innerhalb des Mörtels selbst, die verallgemeinernd (und nicht ganz korrekt) als Kohäsion bezeichnet werden. Diese Bindungskräfte werden durch das Saugvermögen der Ziegel genauso beeinflusst wie das Wasserrückhaltevermögen des Mörtels oder die Staubfreiheit der Steinoberflächen, sind also ein relativ sensibler Parameter. Schon aus diesem Grund ist es bedeutsam, Stein und Mörtel aufeinander abzustimmen und die Bauausführung genau zu überwachen. Neue Entwicklungen wie geklebte Systeme oder Materialauftrag mit Mörtelschlitten versuchen, die bestehenden Unsicherheiten zu reduzieren.
Das Mörtelbett oder die Mörtelfuge ist jedoch nicht nur „Störfaktor“ zwischen den Ziegeln, sondern ermöglicht einen Ausgleich von Unebenheiten schon bei der Herstellung, aber auch den Ausgleich von Spannungsspitzen durch seine Verformbarkeit (Kriechen). Der Ziegelscherben hingegen ist starr und relativ spröde. Neuere Entwicklungen wie die Dünnbettmörtel auf plangeschliffenen Ziegeln oder geklebte Bausteine erhöhen nicht nur die Baugenauigkeit, sondern eliminieren Wärmebrücken durch den schlechter dämmenden Mörtel und vermeiden negative Einflüsse wie eine zu geringe Querdehnsteifigkeit.
Im Bauwerk ist ergänzend ein Zusammenwirken von Mauerwerk mit den Decken gegeben – mit den Forderungen nach Weiterleitung von Kräften und der Verschließung der einzelnen Wandelemente –, sodass in der Gesamtheit ein räumlich stabiles und tragfähiges Gebäude entsteht.
Druckbeanspruchung
Die Druckfestigkeit ist die wichtigste Kenngröße für die Tragfähigkeit von Mauerwerk, sie ergibt sich primär aus den Festigkeiten von Stein und Mörtel. Unter einachsiger Druckbeanspruchung senkrecht zu Lagerfuge entsteht eine Stauchung des gesamten Mauerwerkgefüges bei gleichzeitig dreiachsigem Spannungszustand in Steinen und Mörtel infolge eines ungleichen Querdehnungsverhaltens der beiden Materialien. In der Regel weisen konventionelle oder dämmende Mauermörtel eine höhere Querdehnung als der Mauerstein auf, die sich natürlich wegen der vorhandenen Verbundwirkung nicht einstellen kann und die deshalb Querzugspannungen im Stein erzeugt.

Die Mauerwerksdruckfestigkeit hängt direkt von der Höhe der Lagerfuge ab und erreicht bei dünnen Fugen – mit in der Regel steiferen Mörteln – eindeutig höhere Werte. Dies findet sich bei den in der ÖNORM EN 1996-1-1 angegebenen Wandfestigkeiten wieder. Bei gleicher Steindruckfestigkeit erzielt man mit Dünnbettmörtel eine wesentlich höhere Tragfähigkeit des Mauerwerks wie mit Normalmörtel (M10). Folgende Faktoren beeinflussen das Bruchverhalten von Mauerwerk:
- das Verhältnis von Zug- und Druckfestigkeit des Steines
- das Verhältnis der Querdehnungsmodule von Stein und Mörtel
- das Verhältnis von Querdehnungs- und Längsdehnungsverhalten des Mörtels
- die Fugendicke
- die Steinabmessungen und die Geometrie des Steinquerschnittes
Obwohl es eine Vielzahl von Rechenmodellen zur Ermittlung der Mauerwerksfestigkeit unter Berücksichtigung der beschrieben Parameter gibt, hat sich eine einfache Formel nur unter Heranziehung der jeweiligen Komponentenfestigkeit als praktikabelste Variante durchgesetzt und ist in ähnlicher Form schon seit vielen Jahrzehnten in den Normen verankert.
Druckbeanspruchungen auf Teilflächen
Lokalen Lastspitzen können in homogenen Materialien infolge der Dehnungsbehinderung durch umgebende, unbelastete Bereiche in größerem Maße ertragen werden, als gleichmäßig über den vollen Querschnitt wirkende Spannungen, wodurch lokal auch erhöhte Widerstände auftreten und diese durch Erhöhungen der Wanddruckfestigkeit von bis zum 1,5-Fachen berücksichtigt werden.
Bei modernem Mauerwerk sind jedoch sehr oft keine homogenen Materialien vorhanden, Teilflächenlasten wirken sogar – oftmals ungünstig – nur auf Steinbereiche mit unterproportionalem Tragquerschnitt (z. B. im Inneren eines wärmetechnisch optimierten Ziegels). Deshalb darf bei Teilflächenpressungen, mit Ausnahme von Wänden aus Ziegeln der Gruppe 1, nur die Bemessungsdruckfestigkeit der Wand angesetzt werden.
Es darf immer mit einem unter der Lasteinleitungsfläche beginnenden „Auseinanderfließen“ im darunter liegenden Mauerwerkskörper (Verteilung der Spannungen unter 60°) gerechnet werden. Die üblicherweise angesetzte Lastausbreitung unter 60° findet nur statt, wenn ein entsprechend steifes „Auflager“ vorhanden ist, ansonsten bleibt das Spannungsbild gleich.

Bei sehr kleinflächig wirkenden Spannungsspitzen entstehen durch „Plastifizieren“, das heißt durch „sich der Beanspruchung (teilweise) entziehen“ von hoch belasteten Bauteilbereichen und Mitaktivieren von noch tragfähigeren Bereichen, Spannungsumlagerungen. Der dafür verantwortliche Mechanismus ist das Verformungsverhalten unter Last, welches diese Ausgleiche auslöst. Aus Versuchen erkennt man, dass je kleiner die Teilfläche, desto geringer die der Lasteintragsfläche zugeordnete Stauchung bei gleicher rechnerischer Stegflächenspannung, d. h., es kommt selbst bei den hoch aufgelösten Steinquerschnitten zu nennenswerten Umlagerungen über die Querstege.
Zu große Ausmitten bei lokaler Lasteintragung sind ungünstig, da daraus ungünstig wirkende lokale Zugspannungen in benachbarten Bereichen resultieren können, und mit t/4 beschränkt. Teilflächenbelastungen am Rand von Wänden sind ebenfalls ungünstig, da hier die angesprochene Querdehnungsbehinderung nur teilweise wirksam wird. Bei exzentrischer Belastung ganzer Wände verformt sich die Wand unter Ausbildung von lokalen Spannungskonzentrationen dem eingeprägten Moment entsprechend.
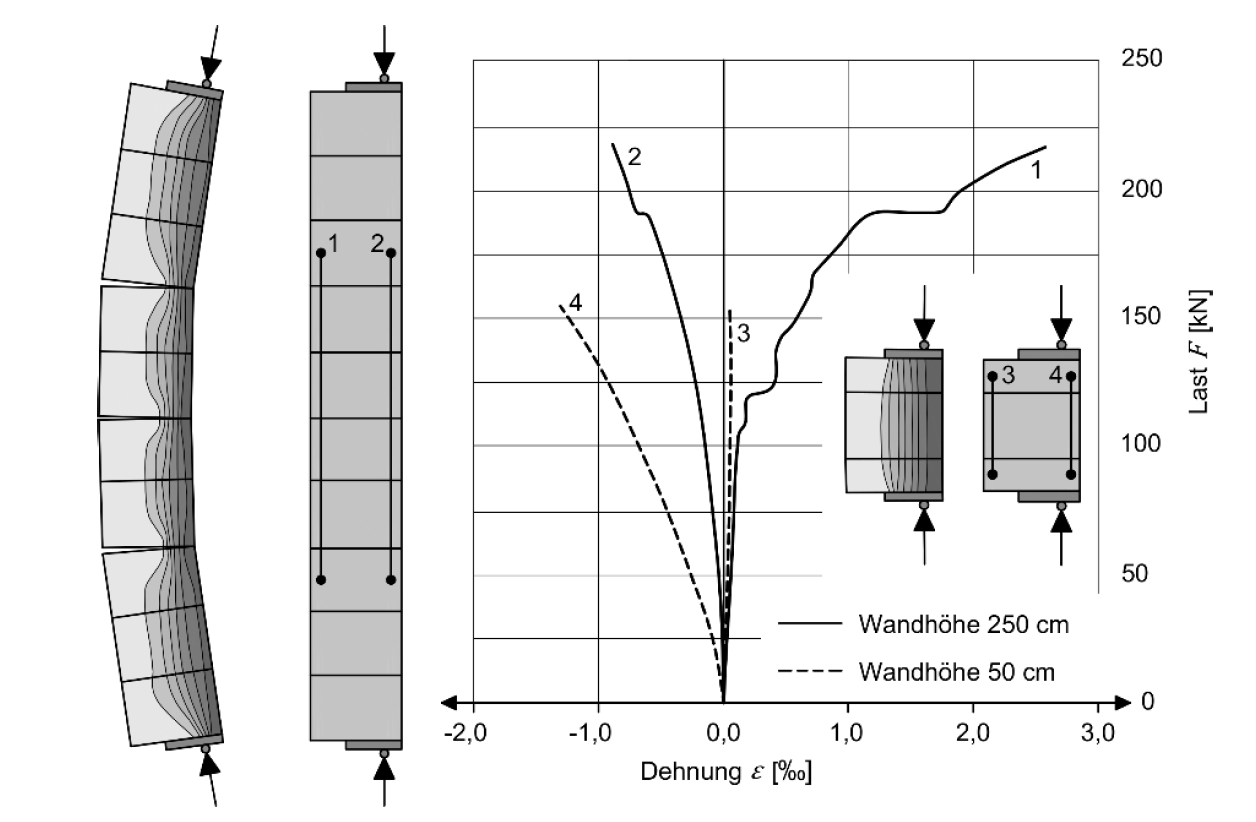
Scherbeanspruchung
Die Scherfestigkeit 𝑓vk, oft als Schubspannung bezeichnet, ist eine wichtige Größe für die Beurteilung der Querkrafttragfähigkeit von Mauerwerk, die insbesondere für den Standsicherheitsnachweis von Aussteifungswänden und Kellerwänden ermittelt werden muss. Das grundlegende Modell des Scherwiderstandes entspricht der Mohr-Coulomb´schen Spannungsgeraden und setzt sich aus zwei Komponenten, Anfangsscherfestigkeit 𝑓vk0 und Reibung μ unter definierter Druckspannung, zusammen. Somit ist streng genommen die Scherfestigkeit eine abgeleitete Festigkeit.
Eine reine Querkraftbeanspruchung kann durch ein „Kleben“ von Mörtel am Stein (Adhäsion in der Kontaktfuge oder der mechanischen Verzahnung durch die Bildung von Kristallen in Porenräumen des Ziegels und durch Eindringen von Mörtel in die Hohlkammern von Lochsteinen) aufgenommen werden. Alternativ ist auch ein Scherversagen im Grundmaterial – Kohäsionsbruch (im Ziegel oder Mörtel) – möglich. Dieser Wert (die charakteristische Anfangscherfestigkeit 𝑓vk0) lässt sich durch zusätzlich wirkende Normalkräfte proportional erhöhen, wobei dieser Proportionalitätsfaktor als Reibungsbeiwert (Haftreibung) μ bezeichnet wird.
Was den Zusammenhang Scherkraft und Verformung betrifft, ist erkennbar, dass die Scherkraft (Scherspannung) ein Maximum schon bei kleinen, im elastischen Bereich liegenden Verformungen erreicht, dann unter Verlust der Haftscherfestigkeit und der Abnahme des Anfangsreibungswinkels (schwächere Rissverzahnung) auf 70 bis 80 % ein annähernd konstantes Niveau erreicht, wo – bei dynamischen Versuchen – auch mehrmalige Lastzyklen abgetragen werden können.
Abbildung 5-05: Arbeitslinie bei Reibungsversagen in der Lagerfuge nach


Biegebeanspruchung
Unter horizontaler Belastung (Erddruck bei Kellerwänden oder Wind) kommt es zu Biegezugspannungen im Mauerwerk. Bei genauerer Betrachtung sind effektive Biegezugspannungen nur im Falle von Bruchebenen parallel zur Lagerfuge eindeutig wirksam. Bei Biegung quer zur Lagerfuge könnten diese zwar in vollständig verfüllten Stoßfugen auftreten – wobei der Verbund Stoßfugenmörtel-Ziegel oft mangelhaft ist. Bei offenen Stoßfugen oder bei Mörteltaschen mit nur 40 % des Querschnitts ist eine Biegemomentenaufnahme nicht möglich. In diesem Fall wird der Biegewiderstand nur über eine Verdrehungsbehinderung in den Lagerfugen – also über die Haftscherfestigkeit der Lagerfugen erzeugt.

| Bruchebene parallel zu Lagerfugen | Bruchebene senkrecht zu Lagerfugen |
Dennoch steht außer Diskussion, dass gut vermauertes Mauerwerk Biegebeanspruchungen in gewissem Maße schadensfrei ertragen kann. Entsprechende Widerstände (Werte 𝑓xk1 oder 𝑓xk2) dürfen nach ÖNORM EN 1996-1-1 auch angesetzt werden. Voraussetzung ist aber, dass das Mauerwerk mit einem normentsprechenden Überbindemaß hergestellt wird. Sogar eine Kombination beider Biegewiderstände zur Momentenabtragung in Plattenebene ist möglich. Auch eine Erhöhung des Biegewiderstandes durch Berücksichtigung von vorhandenen Druckspannungen (z. B. durch einwirkende Wandlasten) darf in Berechnungen eingeführt werden, da diese die auftretenden Zugspannungen „überdrücken“ und zusätzlich den Reibungswiderstand in den Lagerfugen erhöhen.
Hier ist der Eurocode progressiver als die ältere DIN 1053-100 oder auch die ÖNORM B 3350, wo Zugspannungen generell – und somit auch Zugspannungen zufolge Biegebeanspruchung – als nicht aufnehmbar definiert wurden und daher Biegebeanspruchungen nur durch vollständiges „Überdrücken“ der Zugspannungen abgetragen werden konnten.
Zugbeanspruchung
Parallel zur Lagerfuge treten Zugkräfte in Wandteilen z. B. bei Zwängen infolge von Verformungsbehinderung auf. Sofern hier überhaupt eine Berechnung erfolgt, kann die Zugkraftweiterleitung nur über die Reibung in den Lagerfugen und nicht über die Stoßfugen angesetzt werden – ist also streng genommen eine kombinierte Schub-Zug-Beanspruchung der Bauteile.
Aus dem Überbindemaß und dem Reibungsbeiwert lässt sich die Zugfestigkeit parallel zur Lagerfuge unter Beachtung der maximalen Steinzugfestigkeit ermitteln.
Voraussetzung hierfür ist aber, dass das Mauerwerk mit einem ausreichenden Überbindemaß (ü ≥0,4·h) hergestellt wird. Vorhandene Spannungen quer zu den Lagerfugen wirken sich günstig auf die Zugfestigkeit des Wandelements parallel zur Lagerfuge aus.

| Reibungsversagen im Verband | Zugversagen im Stein |
Kombinierte Beanspruchungen
Scheibenschub
Um Horizontalkraftnachweise bei gemauerten Bauwerken führen zu können, muss das Verhalten von gemauerten Wandscheiben bei statischen oder auch dynamischen horizontal wirkenden Kräften bekannt sein.
Eine Wandscheibe trägt gleichzeitig Normalkräfte wie auch einwirkende Horizontalkräfte ab. Daraus resultieren, je nach der Intensität und dem Verhältnis der einwirkenden Kräfte, unterschiedliche Beanspruchungszustände, die auch unterschiedliche Bruchversagen zur Folge haben. Die Beanspruchung in der Scheibe selbst ist naturgemäß nicht gleichartig, sondern abhängig vom Betrachtungsort und von der Geometrie der Steine.
Zur Vertiefung der Kenntnis der maßgeblichen Einflussparameter und zur Überprüfung der Rechenmodelle für den Scheibenwiderstand wurden im Forschungsprojekt ESECMaSE (Enhanced Safety and Efficient Construction of Masonry Structures in Europe) umfassende Untersuchungen gemacht. Dabei wurden sowohl das tatsächliche Verformungsverhalten, die Rissmechanismen und die Verifikation von erwarteten Tragreserven im Vergleich von Ansätzen in den europäischen Normen beschrieben.
Scheibenschub – vereinfachtes Tragmodell
Zur Bestimmung der Schubfestigkeit einer Wand wird das vereinfachte Versagensmodell von Mann/Müller herangezogen. Hier werden das Gleichgewicht und die Beanspruchung an einem Einzelstein in Wandmitte betrachtet und die Versagenszustände bei unterschiedlichen Beanspruchungskombinationen der Wandscheibe definiert. Eine Übertragung von Schubspannungen über die Stoßfuge wird hierbei aus Sicherheitsgründen ausgeschlossen.

Der Grenzzustand der Schubfestigkeit wird erreicht, wenn entweder die Steine (auf Zug oder Druck) oder der Mörtel (auf Schub) versagen. Die Schubfestigkeit von Mauerwerk ist somit, im Unterschied zur Mauerwerksdruckfestigkeit, kein fixer Wert, sondern ist vom jeweiligen Lastzustand abhängig.
- Versagen durch Schub: Bei geringen Auflasten werden bei diesem Versagensmechanismus die aufnehmbaren Scherspannungen – primär in den Lagerfugen – überschritten und es kommt zu Gleitungen und Rissen in den Mauerfugen – entweder gerade oder abgetreppt. Es gilt das Versagenskriterium analog Mohr-Coulomb.
- Versagen bei Überschreiten der Steinzugfestigkeit: Steigen die Auflasten, dann ändert sich die Neigung der resultierenden Kraft und somit die Beanspruchung in der Wand – in den Steinen entstehen schräge Querzugspannungen, die dort zum Aufreißen führen können. In einer vereinfachten Betrachtung kann man die Steinzugfestigkeit als Grenzwert ansetzen.
- Versagen bei Überschreiten der Steindruckfestigkeit: Erhöht man die vertikalen Kräfte weiter (bei gleichzeitiger Reduktion der Horizontalkräfte), dann entstehen stark geneigte Druckstreben im Wandkörper. Als Grenzfall konzentrieren sich die Druckspannungs-trajektorien im randnahen Wandbereich und können dort zum Druckbruch führen. Die Querzugkomponente aus der Neigung vermindert die vorhandene Druckfestigkeit des Mauerwerks. Vereinfacht kann angesetzt werden, dass die aufnehmbare Schubspannung nicht größer als die Differenz zwischen vorhandener Normalspannung und Mauerwerksfestigkeit sein darf, die natürlich nicht überschritten werden kann.
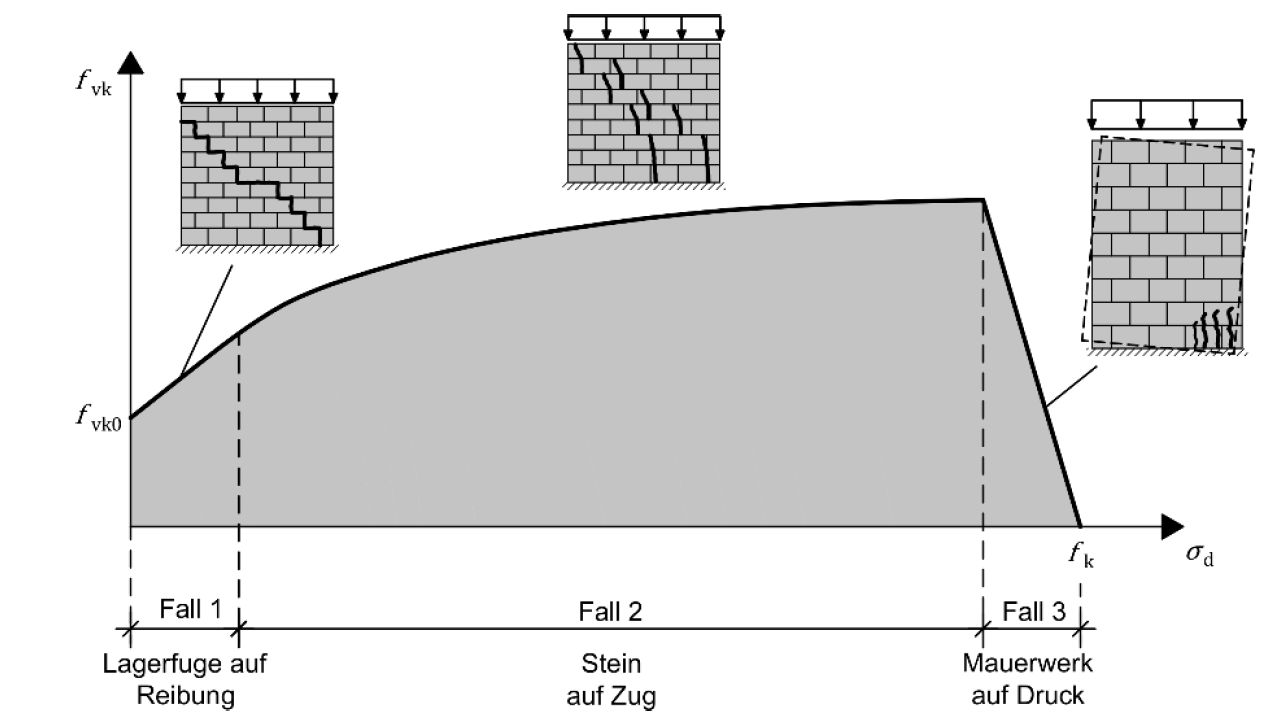

Demgemäß hängt die Schubfestigkeit 𝑓vk von Mauerwerk ab von:
|
𝑓vk0 |
charakteristischer Schubfestigkeit ohne Auflast, Haftscherfestigkeit – Haftkraft des Mörtels am Ziegel bei reiner Scherbeanspruchung. |
| σd | der Druckspannung rechtwinklig zur Schubkraft in der betrachteten Querschnittsebene als Mittelwert der Vertikalspannungen im überdrückten Bereich, der den Schubwiderstand sicherstellt. |
| µ | dem Reibungsbeiwert zwischen Mörtel und Ziegel oder im Mörtel selbst. |
Wandscheiben – Einflüsse auf die Schertragfähigkeit
Bei Anwendung des vereinfachten Modelles von Mann-Müller wird der Widerstand der Wand alleine aus der statisch wirkenden Normalkraft und der anzusetzenden Querkraft ermittelt – nur die Materialparameter und das jeweilige Lastniveau bestimmen die Grenztragfähigkeit. Tatsächlich bestimmt jedoch auch das statische System die Beanspruchung – wegen der daraus resultierenden lastableitenden Zonen und der daraus unterschiedlich ausgeprägten örtlichen Beanspruchungen.

Eine Wandscheibe ohne Auflast mit Horizontalkraft am Wandkopf hat einen sehr kleinen Scherbzw. Schubwiderstand, da ohne zusätzlich wirkende Vertikalkräfte die auftretenden Momente V·ℎ nur in geringem Maße – bis zur Grenze des „Aneinanderhaftens“ der Steine am Mörtel (Haftzugfestigkeit) – aufgenommen werden können.
Reißen die Fugen auf, ist die Fläche für die Reibungsübertragung vermindert und ein ausreichender Reibungswiderstand kann nicht mehr aktiviert werden. Auch bei niedrigem Normalkraftniveau wird durch das Moment, dargestellt als Exzentrizität der Normalkraft, die Zone zur Druckabtragung verkleinert.
Bei höherer Normalkraft N hingegen wird durch die rückdrehende Wirkung das auftretende Moment merkbar verringert und somit die überdrückte Fläche wie auch die aktivierbare Reibung vergrößert – und damit die Möglichkeit, Horizontalkräfte aufzunehmen.
Werden die Horizontalkräfte größer, steigt das Moment – die wirksame Druckzone der schon durch die Normalkraft stärker beanspruchten Wände wird wiederum signifikant reduziert, die Krafteinleitungszone wird örtlich versagen – die Wandscheibe kann über dem Wandfuß aufreiten und rotieren.
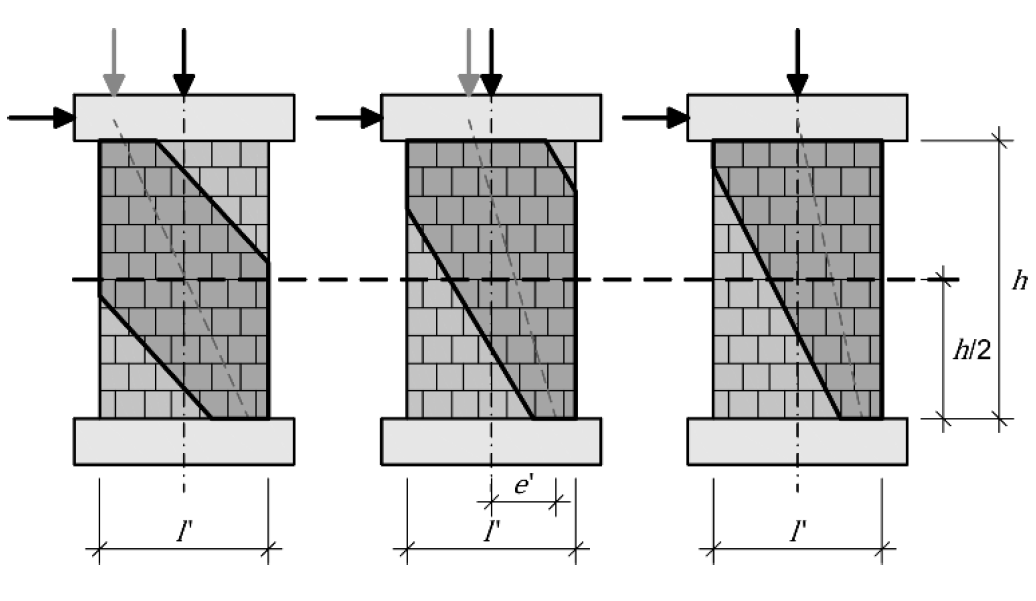
Wird jedoch der Wandkopf – durch steife Bauteile – gegen Verdrehen gesperrt, wird die wirkende Normalkraft gegenläufig verschoben und ohne Veränderung des Lastniveaus das rückdrehende Moment mit seinen günstigen Auswirkungen maßgeblich vergrößert, die Exzentrizität im Wandfuß halbiert. Die Horizontalkraftaufnahmefähigkeit steigt damit signifikant an.
Schon diese „theoretische“ Vorstellung zeigt, dass die Größe und das Auftreten der Hauptbeanspruchungsmechanismen auch von den Lagerungsbedingungen abhängen.
- reiner Schub: entspricht Druck schräg in der Wandscheibe, korrespondierend dazu Zugspannungen in den Steinen
- Zugspannungen in den aufklaffenden Bereichen: Druck und Scheren in Kombination im Wandfuß
Plattenschub und Plattenbiegung
Aus den quer zur Wandebene einwirkenden Horizontalkräften resultieren in den Auflagern der Wand Auflagerkräfte. Die Verteilung dieser Kräfte und die Plattenmomente sind abhängig vom angesetzten Tragmodell der Platte. Kann man von einer guten Einbindung in ausreichend steife Querwände und einer Festhaltung in Deckenebene (Auflager einer steifen Deckenscheibe) ausgehen, dann darf auch eine gemauerte Wand wie eine allseitig gelagerte Platte angesehen und die Plattenmomente dürfen für beide Hauptrichtungen ermittelt werden. Bei Anschlüssen an vertikal tragende Wände kann sogar eine Teileinspannung an den vertikalen Seiten angenommen werden, jedoch muss die Momentenaufnahme nachgewiesen werden.
Die Verteilung der Momente in einer Platte ist vom Stützweitenverhältnis, den Auflagerbedingungen und vom Verhältnis der Biegesteifigkeiten in den Hauptrichtungen beeinflusst. Die Steifigkeit wird unter der Annahme von Rissfreiheit mit voller Größe angesetzt.
Für eine einfache Ermittlung der in den Hauptrichtungen wirkenden Momente werden im EC6 Faktoren für die Stützweitenverhältnisse in Abhängigkeit von den vorhandenen Auflagerbedingungen angegeben. Ein Orthotropiekoeffizient adaptiert die Momentengröße in Richtung der Lagerfugen. Dieser errechnet sich aus dem Verhältnis der Biegezugfestigkeiten des Mauerwerks in beiden Achsenrichtungen. Für die praktische Anwendung sind demnach entweder Prüfwerte erforderlich oder es ist das Verhältnis von 𝑓xk1 zu 𝑓xk2 laut Norm einzusetzen.

© 2018
Der Inhalt dieser Fachbuchauszüge
ist urheberrechtlich geschützt.
zum Buch
