Grundlegende Einflussgrößen bei vertikaler und horizontaler Beanspruchung sind neben den Modellbildungen, das Verbundsystem Stein-Mörtel, die Komponentenfestigkeiten der Materialien aber auch die Ausbildung der Stoß- und Setzfugen bis hin zum Überbindemaß zwischen den einzelnen Mauersteinen. Für die normative Beschreibung der Widerstände von unbewehrtem Mauerwerk werden diese zahlreichen Parameter auf die nachfolgenden Grundparameter reduziert:
- unter Normalkraftbeanspruchung: 𝑓k
- unter Schubbeanspruchung: 𝑓vk
- unter Biegebeanspruchung: 𝑓xk
- Verformungseigenschaften: E-Modul, Schubmodul



Unter Normalkraftbeanspruchung – 𝑓k
Der Basiswiderstand eines Mauerpfeilers oder einer gemauerten Wand gegen Normalkraftbeanspruchung = Druck wird durch die charakteristische Druckfestigkeit 𝑓k beschrieben, wobei diese nach ÖNORM EN 1996-1-1 entweder aus Versuchen abgeleitet oder aber aus den jeweiligen Komponentenfestigkeiten von Mauerstein 𝑓b und Mörtel 𝑓m ermittelt werden kann. Diese rechnerische Ermittlung der charakteristischen Druckfestigkeit aus den Komponenten Mauerstein und Mörtel erfolgt in Abhängigkeit von der Mauersteingruppe und der Mörtelart durch angepasste Formeln.
Druckfestigkeit von Mauerwerk – Definition ÖNORM EN 1996-1-1
Mauerwerksfestigkeit bei Druckbeanspruchung ohne Einfluss der Verformungsbehinderung durch die Druckplatten und ohne Einfluss der Schlankheit und ausmittiger Belastung.
Charakteristische Festigkeit – Definition ÖNORM EN 1996-1-1
Festigkeitswert des Mauerwerks, der mit einer vorgeschriebenen Wahrscheinlichkeit von nur 5% in einer hypothetisch unbegrenzten Grundgesamtheit von Versuchen unterschritten werden darf. Dieser Wert entspricht dem 5 %-Fraktil der angenommenen statistischen Verteilung der Prüfserie einer bestimmten Material- oder Produkteigenschaft. Unter bestimmten Umständen wird ein Nennwert als charakteristischer Wert verwendet.




Die Anwendung der Formel (5-15) ist noch an nachfolgende Bedingungen gebunden:
- Für Mauersteine, die mit Leichtmörtel vermauert werden, darf keine größere Steinfestigkeit 𝑓b als 15 N/mm² in Rechnung gestellt werden.
- 𝑓m darf bei der Verwendung von Leichtmörtel nicht größer als 10 N/mm² sein.
- Für Mörtel darf für 𝑓m kein größerer Wert als 20 N/mm² bzw. 2·𝑓b in Rechnung gestellt werden. Der kleinere Wert ist maßgebend.
- 𝑓b darf bei der Verwendung von Normalmörtel einen Wert von 75 N/mm² nicht überschreiten.
- 𝑓b darf bei der Verwendung von Dünnbettmörtel einen Wert von 50 N/mm² nicht überschreiten.
- Die Mörteldruckfestigkeit von Dünnbettmörtel ist 𝑓m ≥ 10 N/mm².
- Bei Mauerwerk mit Normalmörtel und Mörtelfugen parallel zur Wandebene (Verbandsmauerwerk) muss 𝑓k um 20 % vermindert werden.
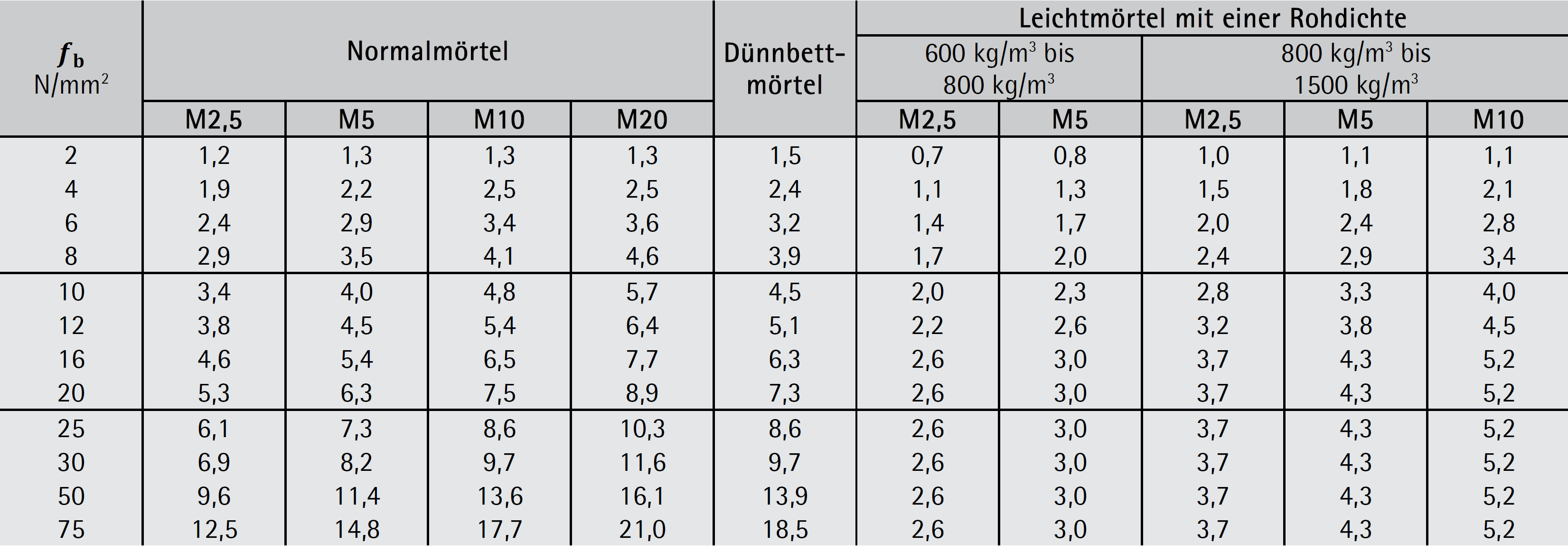
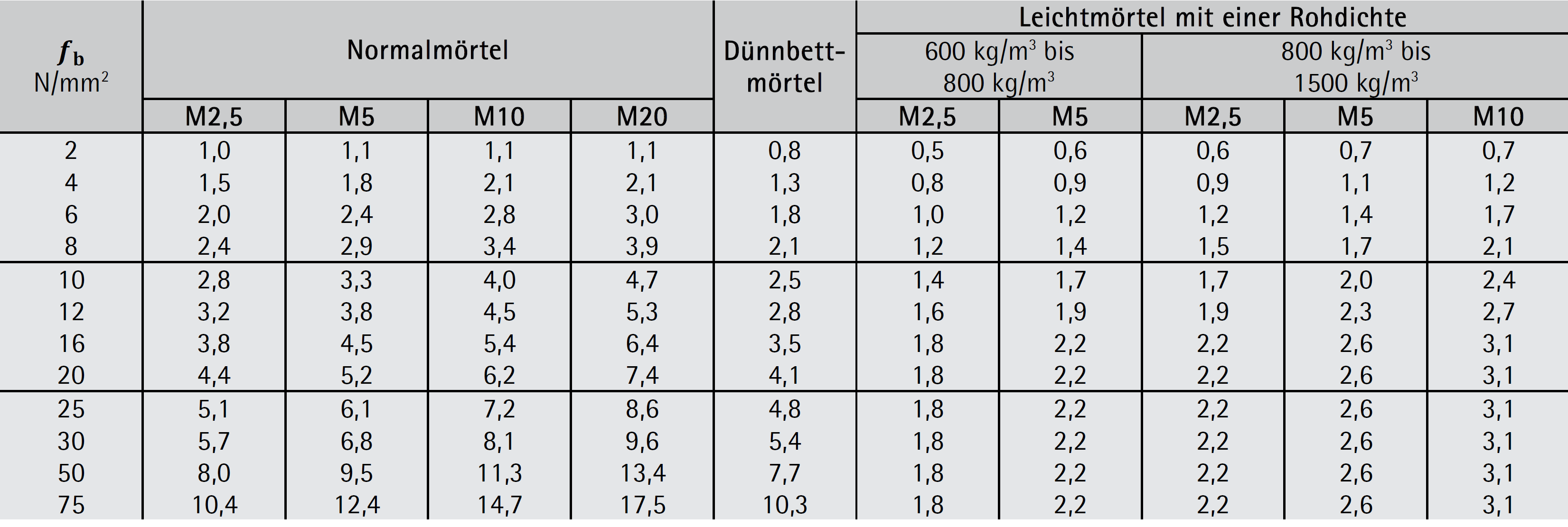
Für ausgewählte Materialkombinationen der Stein- und Mörteldruckfestigkeiten und der Mauersteinart Ziegel kann die charakteristische Mauerwerksdruckfestigkeit auch der Tabelle 5-02 bis Tabelle 5-04 aus der ÖNORM B 1996-3 entnommen werden.

Unter Schubbeanspruchung – 𝑓vk
Die Schubfestigkeit 𝑓vk ist eine wichtige Größe für die Beurteilung der Querkrafttragfähigkeit von Mauerwerk, die insbesondere beim Standsicherheitsnachweis von Aussteifungswänden und Kellerwänden zum Tragen kommt.
Die charakteristische Schubfestigkeit 𝑓vk ist entweder aus Ergebnissen von Versuchen an Mauerwerk für das jeweilige Projekt oder aus einer vorhandenen Datenbasis zu bestimmen oder kann unter Einhaltung definierter Randbedingungen und mehreren Einflussparameter auch aus Normformeln ermittelt werden.
Bei vermauerten Stoßfugen gilt:

Bei unvermörtelten jedoch knirsch gestoßenen Stoßfugen gilt:

Gleichzeitig darf die Schubspannung 𝑓vk einen Grenzwert von 6,5 % der Steindruckfestigkeit 𝑓b (bei voll vermauerten Stoßfugen) bzw. von 4,5 % bei knirsch gestoßenen Stoßfugen – als Grenzwert für ein mögliches Schrägzugversagen der Wand im Stein – nicht überschreiten.
Auch die charakteristische Anfangsscherfestigkeit (Haftscherfestigkeit) 𝑓vk0 von Mauerwerk sollte idealerweise aus Versuchen nach ÖNORM EN 1052-3 oder ÖNORM EN 1052-4 ermittelt werden, es dürfen jedoch – unter der Voraussetzung, dass die verwendeten Mörtel keine Zusatzstoffe oder Zusatzmittel beinhalten – die in der Norm angegebenen Werte ebenfalls angesetzt werden.
Sie beschreibt die Haftkraft des Mörtels in sich (Kohäsionskraft, auch bei Eindringen von Mörtel in die Hohlkammern von Lochsteinen) oder am Ziegel (Adhäsion, in geringem Maße auch eine mechanische Verkrallung durch die Bildung von Kristallen in Porenräumen des Ziegels) bei reiner Scherbeanspruchung ohne Auflast.

Zwischenwerte für die Mörtelfestigkeiten von M1 bis M10 sind linear zu interpolieren. Für Mörtelfestigkeiten unter M1 ist der Ansatz einer Anfangsscherfestigkeit nicht zulässig.
Unter Biegebeanspruchung – 𝑓xk1, 𝑓xk2
Die charakteristischen Biegefestigkeiten 𝑓xk1 und 𝑓xk2 von Mauerwerk sollten durch Versuche (siehe Biegezugprüfungen) nach ÖNORM EN 1052-2 an Mauerwerksprüfkörpern ermittelt werden, können jedoch auch aus den Normtabellen entnommen werden.



Unter Zugbeanspruchung
Vorerst ist festzuhalten, dass es keine Ansätze nach ÖNORM EN 1996-1-1 zur Berücksichtigung von Zugspannungen im Mauerwerk gibt. Das heißt, reine Zugspannungen dürfen im Mauerwerk nicht auftreten bzw. es ist nicht ausreichend gesichert, dass solche Beanspruchungen abgetragen werden können. Tatsächlich treten Zugspannungen parallel zur Lagerfuge in Wandteilen, z. B. bei Zwängen infolge von Verformungsbehinderung oder im Zuge von Lastumlagerungen auf. Sofern hier überhaupt eine Berechnung erfolgt, darf die Zugkraftaufnahme nur über die Reibung in den Lagerfugen angesetzt werden – ist dann also streng genommen überhaupt keine Zugbeanspruchung der Bauteile. Alternativ würde, wenn der Verbund in der Lagerfuge sehr gut und die Steinzugfestigkeit sehr klein ist, ein Versagen auch durch „Zerreißen“ der Steine erreicht. Dieses Versagensmodell ist in der DIN 1053-100 beschrieben.
Die vom Mörtel aufnehmbare Schubspannung wird auch hier durch die Druckspannung σD senkrecht zur Lagerfuge bestimmt, so, dass sich die Zugfestigkeit über die Haftscherfestigkeit 𝑓vk0 und einen Reibungsanteil µ ermitteln lässt. Will man die Zugkraft in diese fiktive „Zugspannung“ umrechnen, gilt Formel (5-20). Voraussetzung ist, dass das Mauerwerk den Normvorschriften entsprechend vermauert wurde, also mit einem ausreichenden Überbindemaß (bei Steinhöhen bis max. 25 cm ü ≥0,4≥h oder mind. 4 cm) hergestellt wird. (Bei Steinhöhe >250 mm muss das Überbindemaß mindestens das 0,2–fache der Steinhöhe oder mindestens 100 mm betragen).
Mit dem Überbindemaß ü = 0,4·h und dem Reibungsbeiwert µ = 0,6 ergibt sich der charakteristische Wert der Zugfestigkeit parallel zur Lagerfuge unter Beachtung der maximalen Steinzugfestigkeit max 𝑓x2.

In der ÖNORM EN 1996-1-1 wird für Schubbeanspruchung geregelt, dass der Wert für 𝑓vk0 bei Mauerwerk mit unvermörtelter Stoßfuge nur mit 50 % anzusetzen ist. Im Falle einer Ermittlung der Zugfestigkeit ist diese Regelung, die aus der Erfassung einer Verdrehbeanspruchung der Steine herrührt, nicht sinnvoll und damit nicht anzusetzen.
Wiederholt werden soll, dass die genannte Ermittlung eines Zugwiderstandes eines Mauerwerkskörpers nach derzeitigem Normenstand für keinerlei Tragfähigkeitsnachweise herangezogen werden darf.
Verformungseigenschaften
Traditionelle Mauerwerksbauten werden selten hinsichtlich der Einhaltung der Gebrauchstauglichkeit untersucht, da in der Regel angenommen werden kann, dass bei Erfüllung der Tragsicherheit auch die Gebrauchstauglichkeit gegeben ist. In Einzelfällen, z. B. für die Fugendimensionierung von Vorsatzschalen, ist jedoch das thermisch–hygrische Verhalten durchaus wesentlich.
Feuchte und Temperatur
Das unterschiedliche Verhalten unter Feuchte- und Temperaturbeanspruchung kann zu Zwangsbeanspruchungen und infolgedessen zu unerwünschten Rissen führen, welche im Normalfall als unkritisch für die Standsicherheit angesehen werden können. Die Gebrauchstauglichkeit und das optische Erscheinungsbild jedoch können dadurch negativ beeinflusst werden. Die ÖNORM EN 1996-1-1 gibt dazu für Ziegel nachfolgende Werte an:
- Endwert der Feuchtedehnung –0,2 bis +1,0 mm/m
- Wärmeausdehnungskoeffizient αt = 4 bis 8 ·10-6 /K
Arbeitslinien der Komponenten – Ziegel und Mörtel
Zur Beurteilung der Gebrauchstauglichkeit von Mauerwerksbauten, aber auch für die Entwicklung von Rechenmodellen und Nachweisverfahren werden die Verformungseigenschaften von Mauerwerk und dessen Komponenten benötigt. Die Daten können aus Versuchen oder aber auch aus vorhandenen Datenbanken entnommen werden.
Die Arbeitslinie von Ziegel unterscheidet sich im Druck- und Zugbereich stark voneinander. Unter Druck ist bei Hochlochziegeln ein am Anfang eher lineares (elastisches) Verhalten festzustellen, welches dann bei zunehmender Krümmung der Arbeitslinie das Erreichen des Entfestigungsbereiches anzeigt. Steine mit höherer Druckfestigkeit weisen in der Regel eine größere Steifigkeit (Anstieg der Spannungs-Dehnungs-Linie) wie auch ein ausgeprägteres Sprödbruchverhalten auf. Die Zugfestigkeit liegt zwischen 3 und 10 % der Druckfestigkeit, bei Hochlochziegeln gelten eher die niedrigeren Werte.
Die Form der Arbeitslinie von Mörtel ist prinzipiell ähnlich der von Beton, wobei der Zuschlagsstoff, aber auch das Bindemittel und damit letztlich die erreichbare Druckfestigkeit auch die Steifigkeit und das Maß der Bruchstauchung beeinflussen (siehe Druckbeanspruchung).
Die Werte des Druck- und des Querdehnungsmoduls für Ziegel sind je nach Steinfestigkeit und Steinquerschnitt sehr unterschiedlich. Auch die Art der Messung, die nicht genormt ist, beeinflusst das Ergebnis maßgeblich.
Elastizitätsmodule
Mauerziegel (Vollsteine) 12 000 bis 22 000 N/mm²
Hochlochziegel 2 500 bis 10 000 N/mm²
Normalmörtel 3 500 bis 11 000 N/mm²
Kalkzementmörtel M5 ~ 6 500 N/mm²
Leichtmörtel 1 800 bis 5 000 N/mm²
Der Elastizitätsmodul Em des Mörtels lässt sich auch in Abhängigkeit von der Mörteldruckfestigkeit definieren.

Die für die Tragvorstellung des Verbundsystems Stein–Mörtel wichtige Größe der Querdehnungsmoduls wird analog zum Druck-E-Modul definiert, nur wird anstelle der Längsdehnung die im selben Querschnitt wirkende Querdehnung eingesetzt. Bei Steinen können bei unterschiedlichem Lochbild die Werte in Steinlänge und Breite auch unterschiedlich groß werden.

Der Querdehnungsmodul liegt bei den Hochlochziegeln um das 4– bis 7–fache höher als der Druck-E-Modul, bei Mörtel um das 4– bis 5–fache (je nach Zuschlagsstoff).
Querdehnungsmodule
Mauerziegel (Vollsteine) 55 000 bis 120 000 N/mm²
Hochlochziegel ~ 10 000 N/mm²
Normalmörtel M2 5 000 bis 17 500 N/mm²
Kalkzementmörtel M10 ~ 50 000 N/mm²
Kalkzementmörtel M5 ~ 32 500 N/mm²
Leichtmörtel M5 ~ 10 000 N/mm²
Daraus lässt sich auch ableiten, dass das Zusammenspiel von eher weichen, hoch wärmedämmenden Steinen und Dünnbettmörtel die Wandfestigkeiten günstig beeinflusst. Oftmals wird auch die Querdehnzahl als Verhältnis zwischen Längs- und Querdehnung oder der entsprechenden E-Moduli angegeben.
Querdehnzahl
Mauerziegel (Vollsteine) ~ 0,20
Hochlochziegel 0,11 bis 0,20
Normalmörtel 0,12 bis 0,20
Leichtmörtel bis 0,25
Mauerwerk – Arbeitslinien unter Druckbeanspruchung
Die Spannungs-Dehnungs-Linie von Mauerwerk unter Druckbeanspruchung ist wegen der Mörtelfugen in der Regel nichtlinear. Für Berechnungsansätze darf sie jedoch entweder als linear, parabelförmig, parabel-rechteckförmig (Abbildung 5-20) oder als Rechteck angenommen werden.
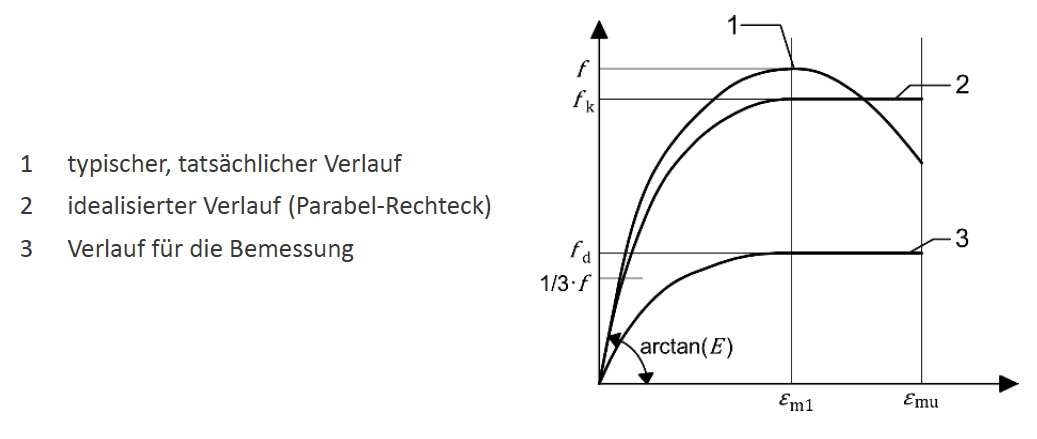
Der Einfluss des Fugenmörtels nimmt naturgemäß mit kleinerer Fugendicke ab. So weist ein Hochlochziegel in Dünnbettmörtel eher sehr sprödes Verhalten auf und entspricht in der Form somit weitgehend der Arbeitslinie des Ziegels.
Der KurzzeitelastizitätsmoduI E als Rechengröße ist der Sekantenmodul bei 1/3 der Maximaltragfähigkeit – beschreibt also das elastische Verhalten – und muss durch Versuche nach ÖNORM EN 1052-1 ermittelt werden.
Liegen keine entsprechend ermittelten Zahlenwerte vor, darf für Verformungs- und Schnittkraftermittlung für Ziegelmauerwerk ein Ansatz von 1000×𝑓k herangezogen werden. Für Langzeitprognosen ist ein infolge Kriechens abgeminderter Langzeitelastizitätsmodul einsetzbar.

Dieser Ansatz mit 1000×𝑓k – also eine direkte Abhängigkeit der Druckfestigkeit – vernachlässigt die Tatsache, dass unterschiedliche Kombinationen von Steinen und Mörtel gleiche Druckfestigkeit aufweisen können, jedoch unterschiedliches Verformungsverhalten haben. Für Verformungsbetrachtungen wird das jedoch akzeptiert.
Jedoch berücksichtigt der Ansatz naturgemäß auch keine Rissbildungsvorgänge infolge von kombinierten Beanspruchungen (z. B. im Erdbebenfall), die eine maßgebliche Abnahme der Drucksteifigkeit bewirken. Für Biegesteifigkeitseinschätzungen bei Horizontalkraftbeanspruchungen (z. B. Erdbeben) kann der angesetzte E-Modul der Schubwände auf 50 % reduziert werden. Diese Abminderung gilt gleichermaßen auch für den Schubmodul.
Wände mit großem Fugenanteil und weichem Mörtel – wie in Altbauten aus Vollziegel die Regel – haben schon im elastischen Bereich einen weit geringeren E-Modul. Aus einem breit angelegten Forschungsvorhaben ergab sich als Wert ein E-Modul von 300×𝑓k und demnach ergaben sich bei Erdbebenbeanspruchung noch weit geringere Steifigkeiten. Der deutlich geringere Elastizitätsmodul kann durch die höhere Anzahl an den geringer festen Mörtelfugen erklärt werden.

Mauerwerk – Arbeitslinie unter Horizontalbeanspruchung
Für die Erfassung der Horizontalkraftbeanspruchung als Scherbeanspruchung ist eine realitätsnahe Beschreibung des Arbeitsvermögens wie auch die Ermittlung der Grenzverformung wesentlich, was ebenfalls in Form einer „Arbeitslinie“ dargestellt wird. Die dabei angesprochene Arbeitslinie beschreibt das Verhältnis der Horizontalkraft und die dabei am Prüfkörper gemessene Horizontalverschiebung am Pfeilerkopf. Das kann sowohl bei einmaliger Lastaufbringung wie unter zyklisch wechselnder Lastrichtung erfolgen.
Für den Schubmodul, der die Ermittlung der Schubverzerrung unter Schubbeanspruchung ermöglicht, wird in der ÖNORM EN 1996-1-1 ein Wert von 40 % des E-Moduls angegeben.

In der nicht mehr geltenden ÖNORM B 4015 wurde auf die Inhomogenität des Verbundkörpers Mauerwerk insofern Rücksicht genommen, als G mit stark abgeminderten Werten von nur 60×𝑓k bis 180×𝑓k angesetzt werden kann, also die Schubweichheit des nicht volumenskonstanten Systems Ziegel–Mörtel besser berücksichtigt wird. Eine Annäherung der Ansätze ergibt sich bei den Nachweisen von Erdbebenkräften, wo die Druck-E-Module auf 50 % reduziert werden können, was in gleichem Maße auch für den Schubmodul gilt – somit wird G mit 200×𝑓k ermittelt.
Arbeitsvermögen und Duktilität
Die Duktilität µ wird aus dem Verhältnis der elastischen zur ultimaten Verformung am Wandkopf errechnet.
Die Verformbarkeit (und damit die Duktilität) wird bei kürzeren Wänden und geringeren Normalkräften größer. Da das Maß der Verformung ein Kriterium für die Energiedissipation ist (Fläche unter der Kurve), ist eine steile Arbeitslinie mit hoher Bruchlast nicht automatisch vorteilhaft und es sind jene Materialkombinationen am günstigsten bzw. auch für die Standfestigkeit der Bauwerksstruktur am besten, wo sich Horizontalkraftaufnahme und gleichzeitig die Verschiebekapazität vergrößern, Bauteile also eine große Duktilität aufweisen.

Auf der horizontalen Achse wird die Verschiebung am Wandkopf, auf der vertikalen Achse die aufgebrachte Horizontalkraft aufgezeichnet. Ke ist die Anfangssteifigkeit Hcr/dcr bei 0,7·Hmax. Die Grenzlast Hu wird nach dem Prinzip der äquivalenten Arbeit errechnet.

Bei zyklischen Versuchen sind die Arbeitslinien – eindeutiger als Last-Verformungslinien tituliert, von der jeweiligen Versagensform, die wiederum durch das Belastungsniveau beeinflusst wird, abhängig. Beim Fugenversagen wird bei der ersten Beanspruchung die Last-Verformungslinie des „Scherversuchs“ erkennbar.
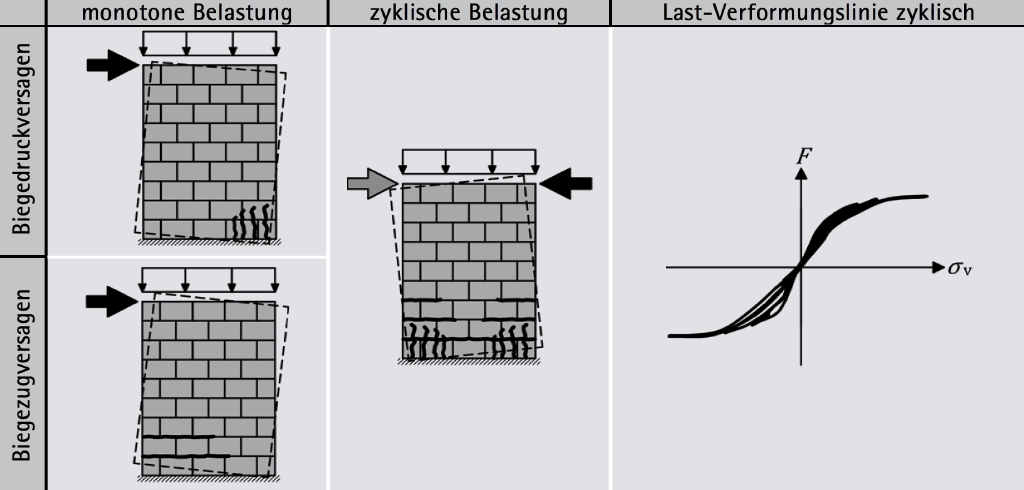
Wichtig für den Widerstand von Mauerwerksscheiben ist, dass bei einem Versagen eine große Energiemenge (= Arbeit = Fläche unter der Arbeitslinie) abgebaut werden kann und somit das Materialverhalten „duktil = günstig“, weil elastoplastisch, ist. Bei einem höherem Normalkraftniveau ist das Verhalten von Schubwänden eher spröde, durch die Risse kommt es dann zu Steifigkeitsabminderungen. Bei schlanken Mauerwerksscheiben kann es rasch zu einem Versagen am Eck der Wandaufstandsfläche kommen, wodurch dann auch die Kopfverformungen maßgeblich zunehmen, der Bauteil reagiert duktil, jedoch ist die Energiedissipation klein.
Geklebtes Mauerwerk
Aus Versuchen an Planziegelwänden ergab sich, dass, im Vergleich zu Mauerwerk mit Dünnbettmörtel, das geklebte Wandsystem eine durchgängig geringere Tragfähigkeit besitzt. Für die Ermittlung der Druckfestigkeit konnte gezeigt werden, dass der in ÖNORM EN 1996-1-1 für Dünnbettmörtel vorliegende grundsätzliche Rechenansatz auch das Tragverhalten von geklebtem Mauerwerk ausreichend gut abbildet. Deshalb wird für die charakteristische Druckfestigkeit nur ein ergänzender Vorwert κ eingeführt sowie werden für die Scherfestigkeit und Biegetragfestigkeiten Werte angegeben.


Planziegel, die mit Schaumklebern verklebt werden, müssen wegen der sehr geringen Fugendicke und des Unvermögens eines Abbauens von lokalen Druckspannungsspitzen ebene, planparallele Lagerflächen, ohne Stufen der Steine zueinander aufweisen. Abweichungen von der Ebenheit wie auch die von der Planparallelität am Stein sind je mit 0,2 % der Diagonalenlänge der Lagerfläche, maximal aber 1 mm beschränkt. Je laufendem Meter Wand darf die Abweichung von der Ebenheit ebenfalls nicht mehr als 1 mm betragen.
Hatte man ursprünglich Zweifel an der ausreichenden Dauerhaftigkeit, ist das mittlerweile kein Thema mehr. Die durchgeführten Untersuchungen zur Beurteilung des Langzeitverhaltens am Verbundsystem lassen im Wesentlichen keine Festigkeitsverluste erkennen und es wird heute erwartet, dass die Standzeit der PUR-Kleber jedenfalls 80 Jahre beträgt. Daher können die über Kurzzeitversuche abgesicherten charakteristischen Werte als Basis für die Bemessung verwendet werden.
Die Schubfestigkeit sowie Biegezugfestigkeit wurden sowohl unter Berücksichtigung von Feuchtigkeitseinwirkung wie auch in Simulation nach Alterung untersucht. Dabei konnten keine Einflüsse auf die Grundwerte abgeleitet werden.
Für Planziegelmauerwerk mit Dünnbettmörtel ist die Bestimmung des E-Moduls nach ÖNORM EN 1052-1 (Sekantenmodul bei einem Drittel der Höchstbeanspruchung) ausreichend genau. Bei geklebtem Planziegelmauerwerk kann jedoch diese Auswertung aufgrund seines frühplastischen Verhaltens zu nicht repräsentativen E-Modulen führen, d. h. Sekantenmodule sind mit Werten zwischen 500×𝑓k und 700×𝑓k. für eine Verformungs- und Schnittkraftermittlung nicht geeignet.
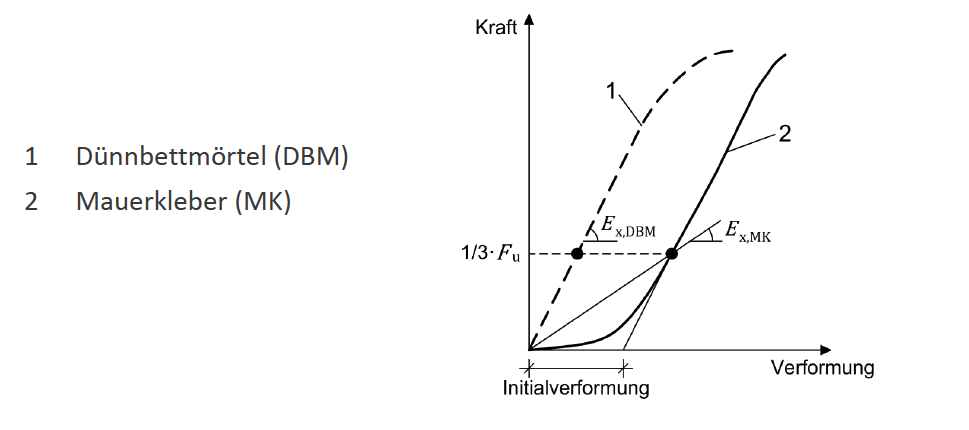
Grundsätzlich wäre zur Beschreibung des Verformungsverhaltens normal zur Lagerfuge zumindest eine bilineare Arbeitslinie erforderlich, wie sie für Trockenmauerwerk aus Kalksandsteinen bzw. Porenbetonsteinen verwendet wird. Für erste Abschätzungen im Grenzzustand der Gebrauchstauglichkeit kann κE als Beiwert für die Ermittlung des Kurzzeitelastizitätsmoduls mit 100×𝑓k bis 200×𝑓k angenommen werden.
Füllziegel
Verfüllziegel mit Beton
Füllziegelwände aus Planziegel werden durch Vermauern mit Dünnbettmörtel oder durch verkleben mit Kunstharzklebern im Verband hergestellt und dann mit Beton verfüllt. Werden die Ziegel korrekt vermauert, dann entstehen durch die vorhandenen Hohlkammern durchgehende Tragsäulen. Somit könnte man in einer sehr sicheren und damit unwirtschaftlichen Betrachtungsweise Füllziegelmauerwerke als reines Planziegelmauerwerk nach der ÖNORM EN 1996-1-1 oder aber als Betonwand nach der ÖNORM EN 1992-1-1 sehen.
Somit kann Füllmauerwerk als Verbundkörper „Ziegel und Beton“ betrachtet werden, wobei nachfolgende Einsatzgrenzen für eine Kombinationsmöglichkeit von Ziegel und Beton definiert werden müssen:
- Dünnbettmörtel der Mörtelgruppe M10 oder höher.
- Werden Kunstharzmörtel bzw. Kunstharzkleber verwendet, ist der Anteil der vom Ziegel übernommenen Traglast zu reduzieren. Das kann durch eine Abminderung der angesetzten Ziegelfestigkeit um 0,61/0,7 ≈ 0,5 realisiert werden.
- Die für die Berechnung herangezogene charakteristische Dauerstandfestigkeit 𝑓ck des Füllbetons darf die doppelte deklarierte Druckfestigkeit des Mauersteins nicht übersteigen.
- Die charakteristische Würfeldruckfestigkeit 𝑓cwk des Füllbetons ist größer oder gleich der deklarierten Druckfestigkeit des Mauersteines.
- Der Füllbetonanteil ist kleiner als 60 % des Wandquerschnittes.

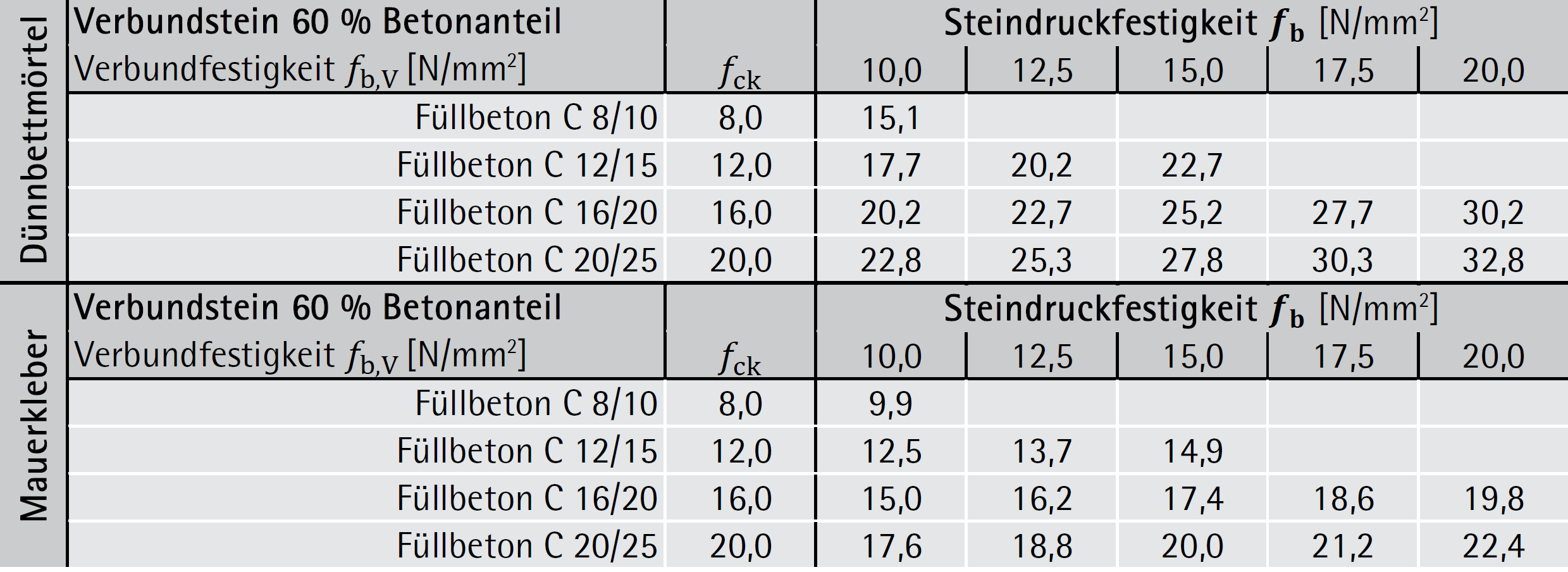
Aus der normierten Steindruckfestigkeit des Verbundsteins kann dann die charakteristische Wandfestigkeit nach ÖNORM B 1996-1-1 für Ziegel der Gruppe 1 und Dünnbettmörtel errechnet werden.

Unterstellt man ein in etwa gleiches Verhältnis Beton und Ziegelmauerwerk, dann erkennt man, dass die Grenzscherfestigkeit bei Ziegel in Bereichen der üblichen Steinausnutzung unter der der Betonfüllung liegt. Es kann deshalb, ohne Risiko, eine Scherkraftaufnahme für den Verbundstein gleich wie an Ziegelwänden der Gruppe 1 mit Dünnbettmörtel bzw. Mauerkleber sowie verfüllten Stoßfugen angesetzt werden.



Planziegel mit Wärmedämmfüllung
Materialparameter - Beschreibung d. Widerstände Eine Optimierung hinsichtlich des Wärmeschutzes stellen mit Dämmstoff gefüllte, mit Dünnbettmörtel vermauerte oder mit Kunstharzkleber geklebte Planziegel dar. Durch das gewählte Lochbild entsprechen die Steine aber nicht der Einordnung der Steine nach Angaben der ÖNORM EN 1996-3 bzw. der ÖNORM EN 1996-1-1 sowie deren nationalen Ergänzungen. Hinsichtlich des Lochanteiles (von ca. 50 bis 65 % würden die gedämmten Ziegel zwar in die Steingruppe 3 passen, jedoch ist die Lochgröße mit Einzel-Lochgrößen von bis über 7 % des Gesamtvolumens über die Normregelung hinausgehend.
Durchgeführte Versuche zeigten, dass das Tragverhalten von Wandprüfkörpern dem von „normentsprechenden“ Steinen sehr ähnlich ist und die genannten Einflüsse auf die Tragfähigkeit in der Wand keine aus dem Normregime herausfallenden Einschränkungen erfordern. Unabhängig vom Herstellerwerk und der damit unterschiedlichen Querschnittsgestaltung sowie von den differierenden Steinabmessungen sind die Bruchbilder aller Prüfpfeiler ähnlich, ebenfalls zeigen die aufgenommenen Arbeitslinien ein grundsätzlich ähnliches Bild.
Auch die Mauerwerksfestigkeit von geklebten Wänden fällt nicht stark gegenüber mit Dünnbettmörtel vermauerten Wänden ab, wobei die Auswertungen zeigen, dass die Wandfestigkeit im Mittel um ca. 10 % geringer ist. Das heißt, für geklebte Ziegel mit Wärmedämmung der (grundsätzlichen) Steingruppe 3 könnte eine geringere Reduktion des Vorwertes 𝜅 = 0,95 angesetzt werden. Verbleibt man bei dem Wert 𝜅 = 0,83 (siehe Geklebtes Mauerwerk), deckt dieser Vorwert das Kollektiv der untersuchten Steine mit ausreichendem Abstand sicher ab.
Grundsätzlich ist der Steinquerschnitt, der die Kontaktfläche mit dem Mörtel und damit die Scherfläche bildet, ähnlich groß wie bei anderen Steinen der Steingruppe 3, ebenso ähnlich ist der Ziegelscherben. Es kann deshalb davon ausgegangen werden, dass auch das Adhäsionsverhalten bzw. die mechanische Verkrallung zwischen Scherben und Mörtel gleichartig wie bei anderen Ziegeln ausbildet. Ergebnisse der Haftscherfestigkeitsprüfungen zeigen eine normkonforme Größe der Anfangshaftscherfestigkeit und des Reibungsbeiwertes.


Bei der Verarbeitung wird jedoch – zur Berücksichtigung der großen Sensibilität hinsichtlich Zerstörungen von Steinschalen – gerade dem Thema Schlitze und Aussparungen besonderes Augenmerk bei der durchzuführenden Kontrolle zu widmen sein.
Bewehrtes und eingefasstes Mauerwerk
Bewehrtes Mauerwerk ist in Österreich nicht stark am Markt vertreten, diesbezüglich fehlt es an einer entsprechenden Bautradition. Mit zunehmend höheren Mauerwerksbauten wird jedoch gerades das Thema Schubkraftaufnahmen immer bedeutsamer. Für diese Beanspruchung ist eine integrierte, Zugkräfte aufnehmende Bewehrung von großem Vorteil. Diesbezüglich ist in der ÖNORM EN 1996-1-1 zu unterscheiden in:
bewehrtes Mauerwerk
Mauerwerk, das Stäbe oder Matten enthält, die in Mörtel oder Beton eingebettet sind, sodass alle Stoffkomponenten durch ihr Zusammenwirken den Tragwiderstand gegenüber den Einwirkungen bilden.
eingefasstes Mauerwerk
Mauerwerk, das mit Bauteilen aus Stahlbeton oder bewehrtem Mauerwerk als Einfassung in vertikaler und horizontaler Richtung versehen ist.
Zusätzlich ist auch vorgespanntes Mauerwerk als Sonderform des bewehrten Mauerwerks genannt.

© 2018
Der Inhalt dieser Fachbuchauszüge
ist urheberrechtlich geschützt.
zum Buch
